Ecosystem Simulator

It was the summer of 2014 when I joined the team. The team size was quite small at the time, with less than 30 people or so, and our game was still in the early stage of development, trying out new things and explore all the possibilities out there. It was a lot of fun.

One day, my boss came along saying "hey, we want to make a realistic in-game ecosystem, would you like to take charge of that?" So what do you mean by a realistic ecosystem? We have a spectacular in-game view of wild lands, but what we wanted was far beyond just looking good. In essence, we wanted to make an in-game ecosystem that resembles the real world.

It would be impractical to plant vegetation and other natural resources manually or randomly. Manual planting would hardly work due to the sheer size of the in-game world. Random planting, on the other hand, would certainly violate manu rules to which the real ecosystem conforms. For example, we wouldn't want to plant banana trees in a snow land or the middle of the ocean.

To make our dream come true, we decided to develop a very sophisticated algorithm to determine the location and the type of plants. The algorithm considers the type of soil, the temperature, the humidity, and other surrounding conditions.

The biggest challenge was the sheer volume of computations it takes to construct a solution. We had tried several ways to make these computations fast and they can be summarized as follows.

First Approach: Matrix Multiplication For Biomass Precalculation

One of the important criteria is something we internally called biomass, which essentially refers to the weight or the predominance of each biological entity. In general, bigger species such as baobab trees have higher biomass whereas smaller species have lower biomass. Each species has different requirements for surrounding biomass; some prefer higher biomasses nearby, others prefer lower biomass in the vicinity.

What we need to take into consideration is the sum of all biomasses within the nearby region when given a particular coordinate, not the biomass of a single coordinate. Calculating the sum of biomasses within a certain region yields a time complexity of O(n²) where n is the radius of the region. Given that we have a square-shaped world (conceptually, in terms of coordinate systems) of a width of m, the total time complexity to calculate the sum of biomasses for all possible locations is O(m²n²) and this can be enormous.

So we started looking into faster methods to calculate the biomasses and came up with a simple yet very effective algorithm, using matrix multiplications, to pre-calculate the sum of biomasses for all coordinates. The resulting matrix is something we call a biomass map, which is essentially a lookup table; for each coordinate, the biomass map stores the sum of the biomasses in the vicinity.

The naive algorithm for matrix multiplication yields O(m³), which has virtually no advantage over our original method. However, there is a faster algorithm for matrix multiplication that yields O(m^2.807).¹ This gives us practical headstart by saving a large number of multiplication operations. Moreover, there is an additional advantage in an engineering perspective: sequential memory access is faster than random access.²

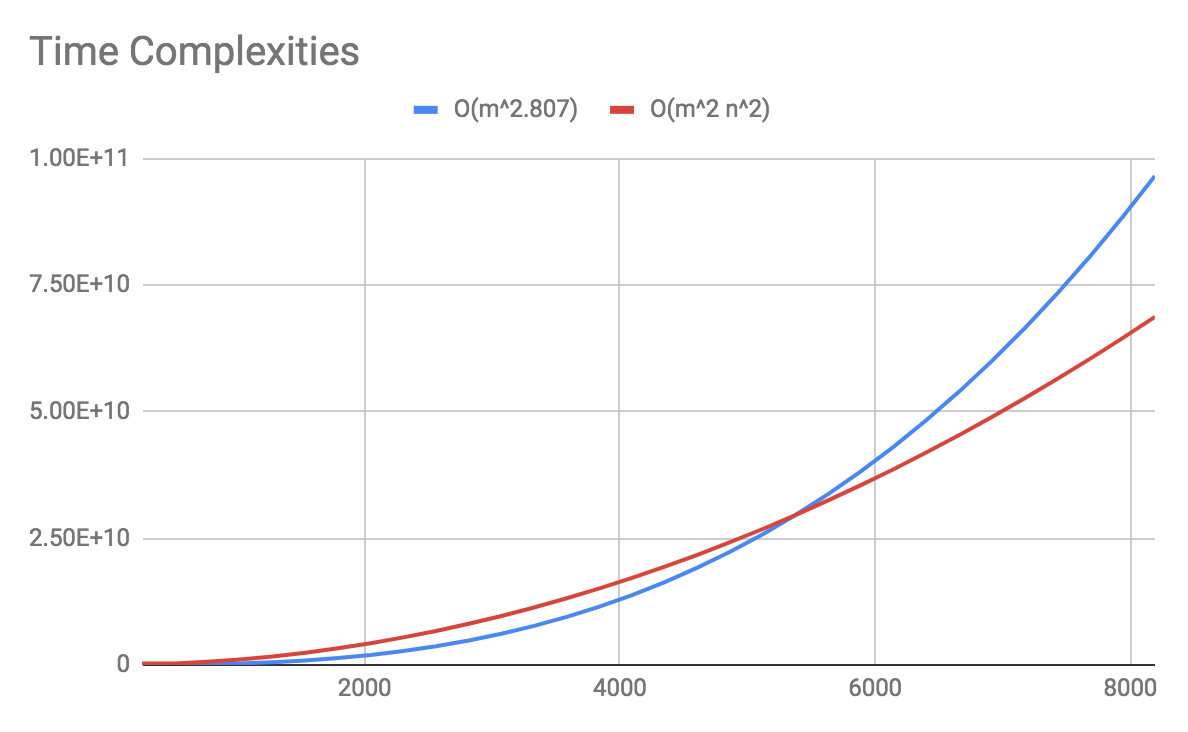
As a result, we were able to achieve a marginal, but measurable³ improvement over our original method. However, this still takes about 30 minutes for a world of 2048x2048, which certainly is a great inconvenience for rapid development. So we decided to look into other options.

Second Apprach: OpenCL

One of irresistible solutions to handle computationally intensive tasks is GPGPU. That is exactly what those GPUs are made for: crunching numbers. There are two major choices when it comes to GPGPU: OpenCL and CUDA. Although CUDA could achieve a higher performance^{[citation needed]}, we opted for OpenCL because of its portability and vendor agnostic aspect.

Long story short, we wrote an OpenCL kernel for biomass maps pre-calculation. As a result, we were able to reduce the 30-minute runtime down to one minute and fifteen seconds, which is a 96% improvement.

Nevertheless, the GPGPU solution offers remarkable performance gains, it comes at a price. Most of all, it was a great engineering challenge; it was difficult to debug, difficult to profile, and difficult to do anything with it. That's probably because we had no prior GPGPU experience whatsoever. Another concern was maintenance and recruiting. Software engineers with GPGPU experience were rare commodities in the job market (at least in 2014, in South Korea).

For this reason, we decided to discard the GPGPU option and move onto a different one, which will be explained in the next section.

Third Approach: Compressed Sparse Row

One characteristic of our game world we could exploit was that it is mostly empty. In many cases, half of the world is deep ocean; players may enter shallow water areas but they are not allowed to swim into the deep ocean, and thus there are no biological entities nor natural resources in the deep ocean. Furthermore, not all land spaces are fully occupied.

This suggests that we might be able to represent our matrices in a compressed sparse row (CSR) format. Then the time complexity will no longer be relevant to the size of the world, but rather the number of biological entities and natural resources in the world.

Fortunately, the math library we use provides compressed spare row representations of matrices and vectors. After switching to CSR, we were able to complete the biomass maps computation in just eighteen seconds, which is slightly slower than the GPGPU solution but certainly acceptable.

Conclusion

Ecosystem simulation is inherently computationally intensive. We have explored several different strategies to minimize the computing time. GPGPU offers lucrative benefits when it comes to large-scale number crunching operations, however, given our circumstances, it was difficult to employ GPGPU for production due to practical constraints. We decided to settle with the compressed sparse row (CSR) representation of matrices as it provides comparable performance to that of GPGPU without having engineering and administrative burdens.

Public Speech On This Topic

More information (in Korean) can be found in the following public speech deck from Nexon Developers Conference (NDC) 2015:

http://ndcreplay.nexon.com/NDC2015/sessions/NDC2015_0063.html